APLICACIÓN DE FUNCIONES
FUNCIONES LINEALES DEL COSTO:
EJEMPLO: Una empresa que fabrica un solo producto se interesa en determinar la
función que expresa el costo total anual y como una función del número
de unidades fabricadas x. Los contadores indican que los gastos fijos
cada año son de $50 000. También estiman que los costos de la materia prima
para cada unidad producida son $5.50 y los costos de trabajo por unidad son
$1.50 en el departamento de ensamble, $0.75 en el cuarto de acabado y $1.25 en
el departamento de empaque y distribución.
Tenemos que:
y = 5.50x + (1.50x + 0.75x + 1.25x) 50 000
Lo que se simplifica como:
y = f (x) = 9x + 50 000
El 9 representa el costo variable combinado por unidad de $9.00. Es
decir, por cada unidad adicional producida, el costo total aumentará $9.
FUNCIONES
LINEALES DEL INGRESO:
Ejemplo:
Una agencia local de renta de autos,
Hurts Renta-Lemon, trata de competir con algunas empresas nacionales más
grandes. La gerencia comprende que a muchos viajeros no les preocupan adornos
superficiales como ventanas, tapacubos, radios y calentadores. I. T. Hurts,
propietario y presidente de Hurts, ha estado reciclando autos usados para que
formen parte de su flotilla. Hurts también simplificó la estructura de tasa de
renta al cobrar una tarifa sencilla de $9.95 por día por el uso de un
automóvil. El ingreso total del año es una función lineal del número de días de
renta de autos de la agencia.
R =ingreso
anual en dólares y d = número de días de renta de autos durante
el año.
R = f (d) = 9.95d
FUNCIONES
LINEALES DE LA UTILIDAD
Ejemplo:
Una empresa vende un solo producto en $65 por unidad. Los costos
variables por unidad son de $20 por materiales y $27.50 por trabajo. Los costos
fijos anuales son $100 000. Elabore la función de la utilidad expresada en
términos de x, el número de unidades producidas y vendidas. ¿Cuál es la
utilidad si las ventas anuales son 20 000 unidades?
Si el producto se vende en $65 por unidad, se calcula el ingreso total utilizando la función lineal.
R(x) = 65x
De modo similar, el costo total anual consiste en costos de materiales, costos de trabajo y costos
fijos:
C(x) = 20x + 27.50x + 100 000
que se reduce a la función lineal del costo
C(x) = 47.50x + 100 000
Por tanto, es posible calcular la función de la utilidad como
P(x) = R(x) - C(x)
= 65x - (47.50x + 100 000)
=17.50x - 100 000
Nótese que P(x) es una función lineal. La pendiente de 17.50 indica que para cada unidad adicional producida y vendida, la utilidad aumenta $17.50. Esto se conoce en los negocios y la economía como utilidad marginal (la suma a la utilidad total de la venta de la unidad siguiente).
Si la empresa vende 20 000 unidades durante el año,
P(20 000) = 17.50(20 000) - 100 000
= 350 000 - 100 000
= 250 000
ANÁLISIS DEL PUNTO DE
EQUILIBRIO
En
el análisis del punto de equilibrio el principal objetivo es determinar el
punto de equilibrio.
Es
posible expresar el punto de equilibrio en términos de 1) volumen de la
producción (o nivel de actividad), 2) total de ventas en dólares, o quizás 3)
porcentaje de capacidad de producción. Por ejemplo, se puede indicar que una
empresa tendrá un punto de equilibrio en 100 000 unidades de producción, cuando
el total de ventas es de $2.5 millones o cuando la empresa opera a 60 por
ciento de su capacidad. Nos enfocaremos sobre todo en la primera de estas tres
maneras.
Los
métodos para efectuar el análisis del punto de equilibrio más bien son
sencillos y directos, y hay maneras alternativas de determinar el punto de
equilibrio. El planteamiento común es el siguiente:
1.
Formule el costo total como una función de x, el nivel de producción.
2.
Formule el ingreso total como una función de x.
3.
Puesto que hay condiciones de equilibrio cuando el ingreso total equivale al
costo total, establezca C(x) igual a R(x) y despeje x. El valor resultante de x
es el nivel del punto de equilibrio de la producción y se podría expresar como
xBE (xBreak - Even; xPunto de equilibrio).
Una alternativa para el paso 3 es
elaborar la función de la utilidad P(x) = R(x) - C(x), establecer
P(x) igual a cero y despejar xBE. El ejemplo
siguiente ilustra ambos planteamientos.
EJEMPLO 1:
Un
grupo de ingenieros se interesa en formar una compañía para producir detectores
de humo. Han desarrollado un diseño y estiman que los costos variables por
unidad, incluyendo materiales, trabajo y costos de comercialización son de
$22.50. Los costos fijos asociados con la formación, operación y administración
de la compañía y la compra de equipo y maquinaria ascienden a un total de $250
000.
Estiman
que el precio de venta será de $30 por detector.
a)
Determine el número de detectores de humo que se deben vender para que la
empresa tenga el punto de equilibrio en el proyecto.
b)
Datos mercadotécnicos preliminares indican que la empresa puede esperar vender
aproximadamente 30 000 detectores durante la vida del proyecto si los
detectores se venden en $30 por unidad.
Determine
las utilidades esperadas con este nivel de producción.
EJEMPLO 2:
Si la curva de demanda está dada por la ecuación Qd = 500-10p y la curva
de oferta está dada por Qs = 10p-100.
a) Halle la cantidad y precio de equilibrio.
b) Construya las gráficas que muestran el equilibrio.
c) ¿Cómo afecta un impuesto sobre las ventas de 10%?
d) Muestre el efecto del impuesto gráficamente.
e) Determine la incidencia del impuesto, es decir, cuánto del impuesto
pagan los consumidores y cuánto los productores.
f) ¿Qué factores influyen sobre el resultado del inciso anterior?
Solución:
a) Halle la cantidad y precio de equilibrio.
En equilibrio Qd =
Qs:
500 - 10p = 10p - 100
-10p - 10p = -100 - 500
-20p = -600
p = -600 / -20
p = 30
Se sustituye para hallar Q:
Q = 500 - 10(30) = 500 - 300 = 200
La cantidad de equilibrio es 200 unidades y el precio es ¢30.
b) Construya las gráficas que muestran el
equilibrio.
c) ¿Cómo afecta un impuesto sobre las ventas de 10%?
Se modifica la función de la oferta:
Qs = 10(p - 0.10P) -100 = 9p - 100
Obsérvese que el 0.10p representa el impuesto que es 10% del precio y
lleva signo negativo porque el impuesto reduce la oferta, no lo aumenta.
Ahora se encuentra el nuevo equilibrio:
9p - 100 = 500 - 10p
9p + 10p = 500 + 100
19p = 600
p = 600/19
p = 31.58
Sustituya (p=31,58) en la ecuación de demanda: Qd = 500-10p
Q = 500 - 10(31.58) = 184.2
El nuevo equilibrio es 184.2 unidades
al precio de ¢31.58.
d) Muestre el efecto del impuesto
gráficamente.
e) Determine la incidencia del impuesto, es decir,
cuánto del impuesto pagan los consumidores y cuánto los productores.
Para responder esta pregunta hay que averiguar
primero cuál sería el precio de la cantidad de equilibrio de 184.2 unidades sin
el impuesto; lo cual se despeja en la función de oferta original:
184.2 = 10p - 100
p = 28.42
Así que el monto del impuesto por
unidad es:
31.58 - 28.42 = 3.16
Esto quiere decir que el gobierno
está recaudando:
¢3.16 x 184.2 = ¢582.07
Antes del impuesto el precio era ¢30 y con el
impuesto el precio es ¢31.58, así que el consumidor está pagando ¢1.58 de
impuesto por unidad, es decir, un total de ¢291.04 (el producto de 1.58 x
184.2). El resto lo están pagando los productores, un total de ¢291.03 (la
diferencia de 582.07-291.04).
f) ¿Qué factores influyen sobre el resultado del
inciso anterior?
El principal factor que influye sobre la incidencia del impuesto sobre
las ventas es la elasticidad precio de la demanda. Mientras más elástica sea la
curva de demanda más paga el productor y mientras más inelástica sea más paga
el consumidor.
FUNCIÓN CUADRÁTICA APLICACIÓN:
EJEMPLO 1: (Decisiones sobre fijación de precios)
La demanda
mensual x de cierto artículo al precio de p dólares por unidad
está dada por la relación x =1350
- 45p El costo de la mano de obra
y del material con que se fabrica este producto es de $5 por unidad y los
costos fijos son de $2000 al mes. ¿Qué precio por unidad p deberá fijarse
al consumidor con la finalidad de obtener una utilidad máxima mensual?.
EJEMPLO 2:
(Equilibrio entre la oferta y la
demanda) Se puede
estimar el equilibrio del mercado entre la oferta y la demanda mediante las
funciones de oferta y demanda en los dos ejemplos pasados al determinar el
precio de mercado que iguala la cantidad surtida con la cantidad demandada. Se
expresa esta condición de equilibrio por medio de la ecuación.
Qs=Qd
Sustituimos y nos que da:
EJEMPLO 3:
(Funciones cuadráticas de la oferta) Encuestas de mercado de proveedores de
un producto particular han dado lugar a la conclusión de que la función de la
oferta tiene una forma aproximadamente cuadrática. Se preguntó a los
proveedores qué cantidades estarían dispuestos a surtir con diferentes precios
de mercado. Los resultados de la encuesta indicaron que con precios de mercado
de $25, $30 y $40, las cantidades que los proveedores estarían dispuestos a
ofrecer al mercado eran 112.5, 250.0 y 600.0 (miles) unidades, respectivamente.
Podemos determinar la ecuación de la
función cuadrática de la oferta al sustituir las tres combinaciones de
precio-cantidad en la ecuación general.
EJEMPLO 4:
Se
estima que en un terreno si se plantan 200 matas de naranjas, la producción
promedio será de 300 naranjas por árbol y que por cada árbol menos que se
siembre la producción aumentará en 3 naranjas por árbol.
a)
¿Cuál es el número de árboles que debe plantarse en el terreno a fin de obtener
la máxima cosecha posible del terreno?
b)
¿Cuál es la producción máxima posible?
) se elimina de la forma normal el término cuadrático y se obtiene la forma reducida:
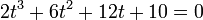, Se procederá a 
(al dividir por 2)
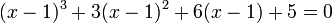, y desarrollando, se obtiene la ecuación en forma reducida 
.
y 
, luego ![u = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} \,](https://upload.wikimedia.org/math/0/2/8/028fb28ea5a3c116efa26ad70b76cfa7.png)
y ![v = \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} \,](https://upload.wikimedia.org/math/3/b/3/3b301c212acc6496fd958be984308ec0.png)
.![t = x - 1 = u + v - 1 = \sqrt[3]{\frac {-1 - \sqrt {5}} {2}} + \sqrt[3]{\frac {-1 + \sqrt {5}} {2}} - 1 \approx -1,3221853546](https://upload.wikimedia.org/math/5/1/3/513472e74ff72db470860f9c127f9789.png)
