FUNCIÓN LINEAL
FUNCIÓN LINEAL
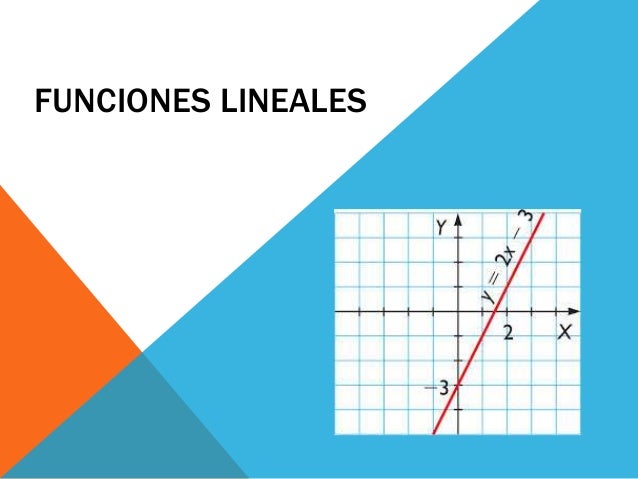
En una función se relacionan dos
magnitudes o variables.
Variable
independiente: Es la
representada en el eje X o de abscisa.
Variable
dependiente: Es la representada en el eje Y o de
ordenada.
Cuando a cada abscisa le corresponde
una sola ordenada, la relación se llama
FUNCIÓN.

DOMINIO
E IMAGEN

Dominio
de f: Es el conjunto
de valores que puede tomar la Variable Independiente.
Imagen
de f: Es el conjunto
de los valores que toma la variable dependiente.
Dominio es el intervalo [ 1, 10 ]
Imagen es el intervalo [ 2, 8 ]
FUNCIÓN CRECIENTE
Es creciente cuando su gráfica leída de izquierda a derecha es
ASCENDENTE.
Esto significa que al aumentar la variable X también aumenta la variable
Y

FUNCIONE DECRECIENTE
Es decreciente si su gráfica es
DESCENDENTE.
Esto significa que al aumentar la
variable X, la variable Y disminuye.

INTERVALOS DE CRECIMIENTO
Las funciones poseen tramos donde crecen y otros donde decrecen.
f es decreciente en [a,b] f es creciente en [b,c]
ECUACIÓN DE LA RECTA
y=mx+b
EJEMPLO: Teniendo en cuenta la siguiente función y= 2x+4 hallar el dominio, rango y realizar una gráfica lineal:
Para x = -2 tenemos:
Y-2=
2 (-2)
+ 4
Y-2=
- 4 +
4 = 0
Para x = -1 tenemos:
Y-1=
2 (-1)
+ 4
Y-1=
- 2 +
4 = 2
Para x = -1 tenemos:
Y0= 2 ( 0 ) + 4
Y0= 0 + 4 = 4
Para x = 1 tenemos:
Y1= 2 (1) + 4
Y1= 2 + 4 = 6
Para x = 2 tenemos:
Y2= 2 (2) + 4
Y2= 4 + 4 = 8
Tenemos:
F(x)
|
0
|
2
|
4
|
6
|
8
|
x
|
-2
|
-1
|
0
|
1
|
2
|
Gráfica:
Otra forma de resolverlo Ejemplo 2:
Es Esta
ecuación es un ejemplo en donde no se identificarán dos puntos diferentes al
asignar a cada variable el valor de 0 y despejar la variable faltante. ¡Observe
lo que ocurre! Si x = 0.
Ambos
casos produjeron el mismo punto (0, 0). Por ende, para identificar un segundo
punto, se debe dar un valor distinto de cero a una de las variables. Si se
supone que x = 7.
Entonces, dos miembros del conjunto solución son (0, 0) y
(7, 4), ilustra la gráfica de la ecuación.
FORMA PUNTO-PENDIENTE
Un tipo
de ecuación lineal es la forma punto-pendiente, la cual nos proporciona la pendiente de una recta y las
coordenadas de un punto en ella. La forma punto-pendiente de una ecuación
lineal se escribe como 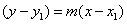 . En ésta ecuación, m es
la pendiente y (x1, y1) son las
coordenadas del punto.
. En ésta ecuación, m es
la pendiente y (x1, y1) son las
coordenadas del punto.
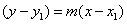 . En ésta ecuación, m es
la pendiente y (x1, y1) son las
coordenadas del punto.
. En ésta ecuación, m es
la pendiente y (x1, y1) son las
coordenadas del punto.
Veamos de
dónde es que viene ésta fórmula de punto-pendiente. Aquí está la gráfica de una
recta genérica con dos puntos trazados en ella.
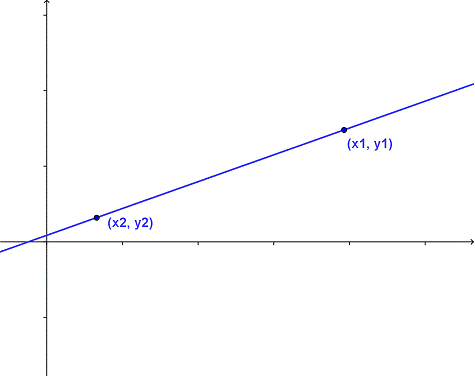
La pendiente de la recta "aumenta conforme va". Ése es
el cambio vertical entre dos puntos (la diferencia entre las coordenadas en y) dividida entre el cambio horizontal sobre el mismo segmento
(la diferencia entre las corneadas en x). Esto puede escribirse como:
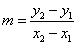 formula de la pendiente donde:
formula de la pendiente donde:
La
ecuación de la recta que pasa por un punto (x1, y1) con pendiente m en
la forma punto-pendiente es:

y – y1 = m(x – x1).
EJEMPLO 1:
Encuentre la ecuación de la recta que pasa por los
puntos (3,2),(4,3) Primero encontramos el valor de la pendiente:
Formula que vamos a utilizar:
Pendiente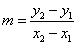
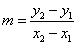
Ecuación de la recta y – y1 = m(x – x1).
Gráfica:

Gráfica:

Ejemplo 3:










0 comentarios: